
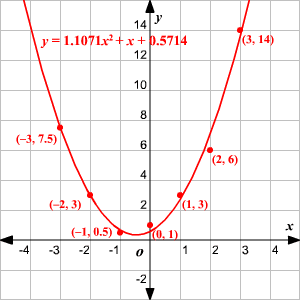
While the tables and equations above may seem intimidating, with a little practice, you'll be a pro at finding quadratic regression in no time. The graphs of quadratic functions have a nonlinear U-shape with exponential curves on either side of a single intercepting y-value. However, if that option is not available, follow the steps above. Luckily there are plenty of websites that provide online calculators that make solving the quadratic regression model much easier. Quadratic Regression is a tough method to tackle by hand. Insert these values (rounding to the 3rd decimal point) into our quadratic equation: Solve for a, b, and c by isolating each of these variables using an online calculator.

Using the matrix equation, fill in all the sums: For example, ∑xi^4 would be the sum of column x^4, 9,669. This Quadratic Regression Calculator quickly and simply calculates the equation of the quadratic regression function and the associated correlation. ∑ represents the summation, meaning that you will plug the relevant sum into the equation. You’ll want to use Microsoft Excel or a calculator for this step:Īt the bottom of each column, calculate the sums:īelow is the matrix equation for determining the parabolic curve. When you plug these values into a graphing calculator they should form a parabola:Ĭreate 5 additional columns for 
This is demonstrated by the graph provided below. Furthermore, the quadratic formula also provides the axis of symmetry of the parabola. The x values found through the quadratic formula are roots of the quadratic equation that represent the x values where any parabola crosses the x-axis. Recall that the ± exists as a function of computing a square root, making both positive and negative roots solutions of the quadratic equation. Below is the quadratic formula, as well as its derivation.įrom this point, it is possible to complete the square using the relationship that:Ĭontinuing the derivation using this relationship: Only the use of the quadratic formula, as well as the basics of completing the square, will be discussed here (since the derivation of the formula involves completing the square). A quadratic equation can be solved in multiple ways, including factoring, using the quadratic formula, completing the square, or graphing. For example, a cannot be 0, or the equation would be linear rather than quadratic. Step 2: Now click the button Solve to get the factors. Sometimes linear regression doesnt quite cut it particularly when we believe that our observed relationships are non-linear. The numerals a, b, and c are coefficients of the equation, and they represent known numbers. The procedure to use the quadratic factoring calculator is as follows: Step 1: Enter the coefficient of the quadratic equation in the input field. Where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant. In algebra, a quadratic equation is any polynomial equation of the second degree with the following form:
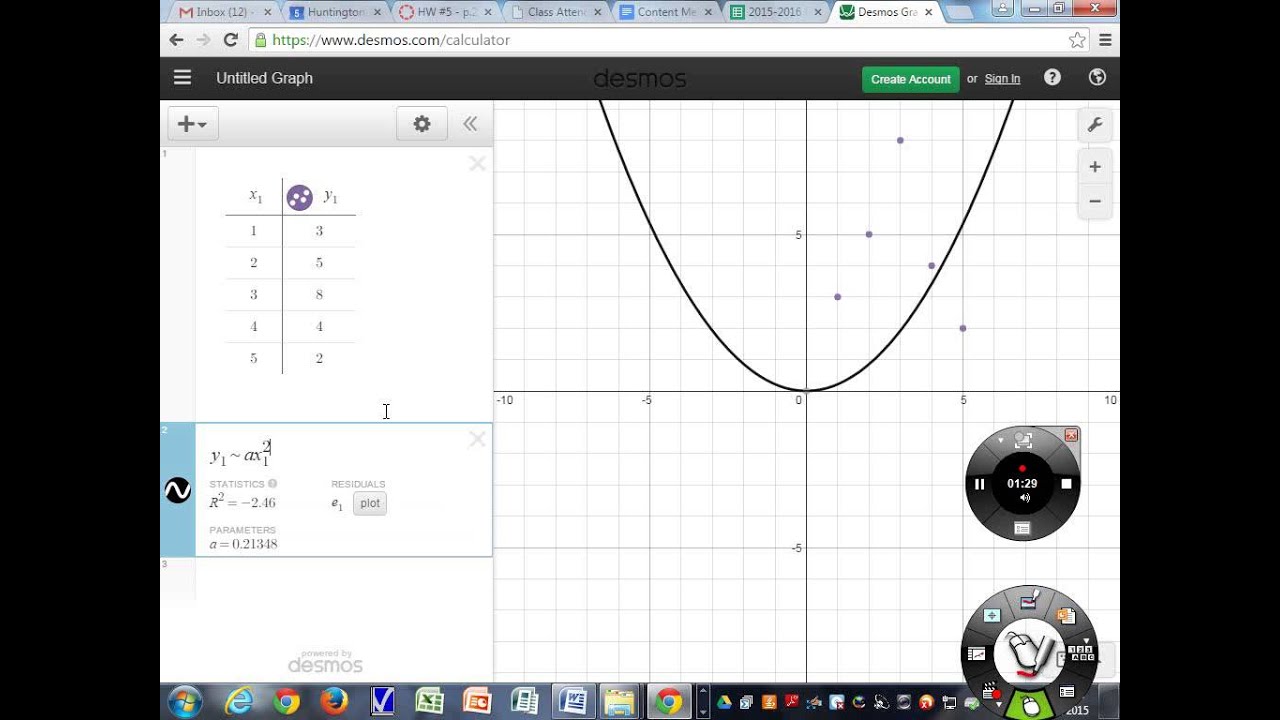
Fractional values such as 3/4 can be used.


 0 kommentar(er)
0 kommentar(er)
